Value Vector: A Scaling Law for Packing & Moving

How movers fight entropy one box at a time.

We’ve all done it.

At some point in our 20s, we convinced ourselves that our apartment is not that big, and we don’t have that much stuff, and that it is totally reasonable to enlist just a few friends to help us pack up our apartment and move on to the next location…

Only to realize after the fact that:

1. Movers are only $100-$150 per hour,

2. They are 3 times more efficient than you and me, and

3. The disgruntled friends and your strained lower back really were not worth the trouble.

However, there’s a challenge: how could you have known from the outset how long it was going to take? Absent a prediction, we always convince ourselves that it won’t take much time (more on this in a future newsletter).

The actual truck we used to move this weekend.

This weekend, I found myself yet again helping someone move — which motivated me to write this the newsletter, so my future self remembers that:

1. packing always takes longer than you expect, and

2. once you can afford it, you should always hire movers.

So in this second edition of Value Vectors, we will gain some intuition for how long it should take to pack - informed by physics. Hopefully with a little math, this can help you save some money in the future¹; or at the very least appreciate that $100/hour is absolutely worth it!

Some Background:

After my first thermodynamics class in undergrad, and my fifth moving experience, I was finally able to fully understand why moving was so painful. Equipped with a little physics and math, I built a model that answered the age old question:

The Packing Question: How long will it take to pack up your apartment?

To answer this, the key concept we need to understand is Entropy. This physical quantity is often poorly represented — so I will give a simple definition that is relevant for right now:

Entropy is the number of ways that a system can be shuffled around.

Roughly speaking, Entropy of a system goes up when:

1. There is more space to push objects around,

2. The number of objects increases,

3. Small objects are placed inside of large objects (thereby creating more space, and a nested structure that will need to be undone).

Left panel: low entropy, Right panel: high entropy

Due to the combinatoric nature of these three principles, a system is statistically much more likely to be in a high entropy state (by random chance) than it is to be in a low entropy state (i.e. something like the right panel above is much more likely). This principle of high entropy being statistically preferred, is known as the second law of thermo, which states:

Entropy tends to increase. To decrease the entropy of a subsystem, one must exert work on a subsystem.

How is this relevant for packing?

To move your personal items from a large diffuse space (your apartment, high entropy) to few dozen compact spaces (boxes), you have to (1) create a mental framework for how to consolidate the items, and then (2) execute and physically realize the plan — both which requires work and energy!

As it turns out, these three knobs that tune entropy along with the second law of thermo suggest a rather simple model for the time it should take to pack (mathematical details omitted).

Let’s see this in practice.

The Model:

Informed by these principles, the model takes three inputs:

1. The duration of time you have lived in the space (as measured in years)

2. The area of the living space (as measured in thousands of square feet)

3. The “nestedness” which can be expressed as a Gini Ratio - this determines how varied your personal belongings are.

The duration of time and area are pretty self explanatory. However, the Gini Ratio (GR) requires some explanation.

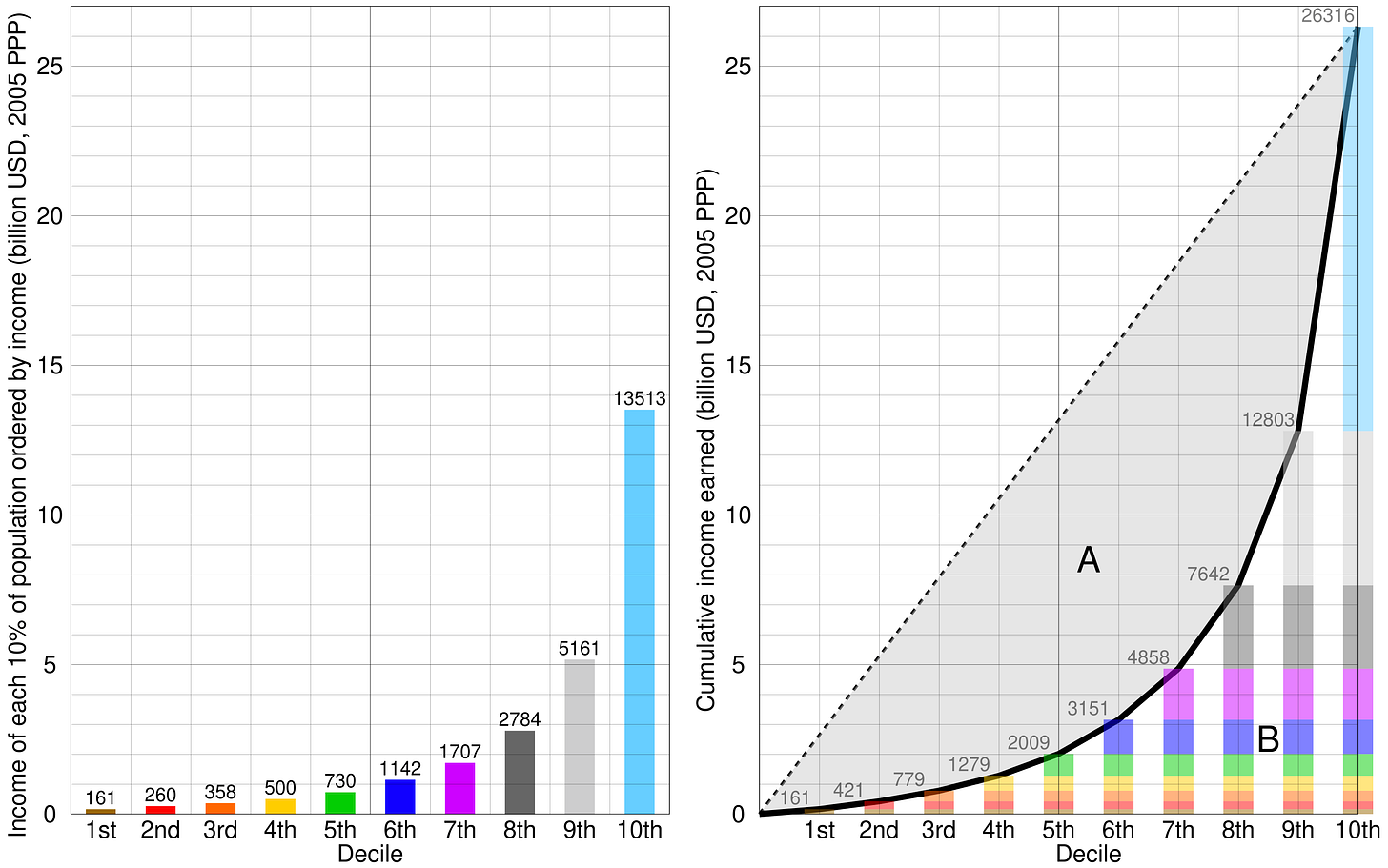
Normally GRs are computed by ordering all incomes in an economy, building a cumulative income curve, and then taking a ratio between areas bisected by the curve (pictured below):

In contrast, a Gini Ratio for packing lists all the items in order by their weight, builds a cumulative weight curve, and then divides the areas bisected by this curve.

A low Gini means that most items are about the same size (like an apartment filled with just furniture) — so the distribution of weight by item is very equal.

Whereas a high Gini means that in addition to the furniture, your apartment is filled with trinkets, knick-knacks, and many many spoons — so the distribution of weight by item is very unequal.

We could get more precise with this definition, but to streamline this newsletter, consider the following visuals for low and high Gini Ratios for an apartment:

Low (Gini = 0.25 - Marie Kondo level)

Medium (Gini = 0.5 - it’s not busy, it’s lived in)

High (Gini = 0.75 - so college)

Yikes (Gini = 1.0 - honey, where’s the cat??)

Feel free to calculate your own personal Gini index for your living space and report below! (I peg myself at about a 0.55).

With this, informed by an understanding of how entropy increases given the size of a room, and number of items, I give you a Model for Packing:

\(\boxed{T(G,Y,A) = e^{G}\,\text{log}_2(1+ Y)\text{log}_2(1+ A) } \)

The inputs of this model are:

1. G - the Gini Index for your personal living space (be honest with yourself).

2. Y - the number of years you have lived in the space (it can be a decimal).

3. A - the floor area of your home (in thousands of square feet - so 3400 sqft, A = 3.4, and 700 sqft, A = 0.7).

The output is simply:

T - the times as measured in the number of human workdays it will take the average person to pack (and I mean full 10 hour workdays).

So if you have some friends, you can divide by the number of people helping, and that gives your expected time to pack.

Some Model Outputs:

Here are some simple contour plots I made to give you a sense of how the number of work days (boxed in grey) change with the input variables - note the axes change between plots:

Try to find where you stand with your current living arrangement! If you’re not on the plot, try plugging some values into the equation for yourself :)

So why is packing so hard, but unpacking easy?

This is also something the we can understand through the second law of thermodynamics.

Every moving procedure has four chronological steps:

Order of Moving:

1. Packing (Old home —> boxes)

2. Loading the car/truck (boxes from old home —> to truck)

3. Unloading the car/truck (boxes from truck —> new home)

4. Unpacking (boxes —> new home)

We can clearly understand this in terms of entropy. Let’s write out items in the chronological list above in terms of their entropy, as follows:

Absolute Entropy:

1. New home (usually larger, highest entropy)

2. Old home (usually smaller, lower entropy)

3. Moving Truck (smallest entropy, unless you live in NYC)

Now, we can understand why the worst part of every move is packing the old home: it is the largest decrease in entropy, and thus requires the most work.

Change in Entropy:

1. Unloading (large increase, careless placement, easy)

2. Unpacking (increase, careful placement, easy-ish)

3. Loading (decrease, careless placement, hard-ish)

4. Packing (large decrease, careful placement, hard)

Since it is energetically hard to carefully decrease entropy in a subsystem, whereas it is energetically easy to carelessly increase entropy:

In closing…

Packing is hard and annoying - so just leave it to the professionals. Trust me. They really have perfected this.

But if you really want to do it yourself, just remember the Model for Packing and you will at least know what you’re getting into:

\(\boxed{T(G,Y,A) = e^{G}\,\text{log}_2(1+ Y)\text{log}_2(1+ A) } \)

Of course, as a good scientist, I admit there could be modifications needed. So tell me, what about you? Do you find that it takes about this many days given your past packing experience?

Comment below, and we can try to empirically constrain the scaling law with some real data!

1. After all, this is Math Meets Money.